30) Unbounded Solutions - When the Answer is Infinity

Fancy an infinite amount of money? UNBD as a solution status is offering you just that – but unbounded solutions are not very likely to be prove true out in the real world so they are no better a basis for a plan than an infeasibility. They are a little easier perhaps to resolve, however, since they are a fairly clear indication of a modelling error.   Unboundedness means that you are missing a constraint on some option, or combination of options, that contribute value to the objective function.  For example if you have a purchase in your model to buy something that you can also sell  - whether because the option is real or just to maintain feasibility – and the buy price is lower than the sales price then the LP will do as much of it as it can.  If there is a limit on either the purchase or the sale, then the problem is bounded and could produce an optimal solution.  However, if there are no limits on either of these activities, then the solution  would be unbounded.

This is why the g5 input panel for utility purchases and sales gives you an error if you can buy electricity at 0.06 $/Kwh and sell it for 0.07.

 This sort of checking however, isn’t done for the purchases and sales of streams, as those appear on different panels.  The PGM has some code for detecting problems during matrix generation and there is also a matrix generation option to raise the purchase prices automatically, but, alas, on trying to make examples for this note, I found that they have fallen into disrepair – so that is something on my to-do list.   In any case, it is not practical to make a complete pre-optimization check for unbounded structures, as in many cases it depends on indirect relationships between variables, and so would be very time consuming compared to letting the optimizer find it.

My unbounded example consists of a purchase at one location, transportation to another location, and a sale there. The purchase price plus the transportation costs are less than the sale price at the destination – and there are no limits on the amounts bought, transported or sold. The reports will tell us that the solution was unbounded, but don’t give any further details (another item for the to-do list). The optimizer solution  (See #29 The Solution Print – It’s the Answer), however, will tell you which vector (column, variable) is causing the problem. The format of this depends on the optimizer.

HSLP marks the vector status as AT ++ in the solution prints in the LST / SPR  files, like so:

 
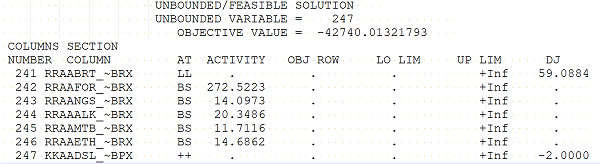
KKAADSL_~BPX is the purchase of diesel at location KK.  (See #16 Decoding Matrix Row and Column Names).  The annotated solution print file (.SPA) will help with understanding names, but does not provide as much information as the optimizer log about what is unbounded.

 

HXPRESS also uses the ++ for “At” in the solution and gives some useful messages in the Optimizer Log File step in the LST file.

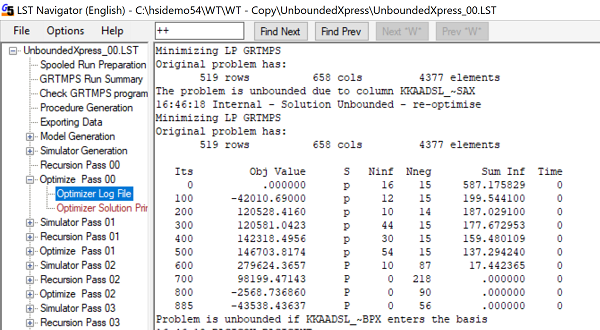
Our attention is also drawn to the sale vector, KKAADSL_~SAX.

H/CPLEX gives similar information in its log file. (“Dual infeasible” is another way of saying its Unbounded.). It does not, however, use the ++ in the solution print.  

 

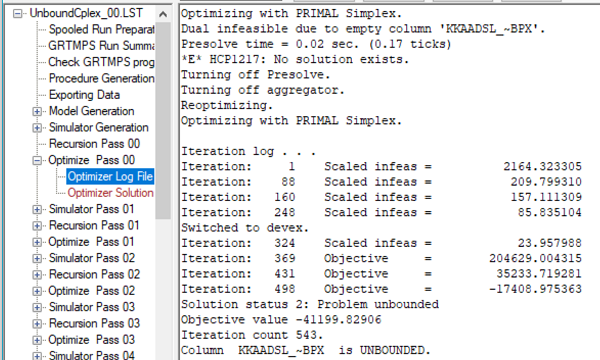
Once you know what is unbounded, the solution is very simple.  Add a constraint.  The best way to do that depends on what the vector represents. 

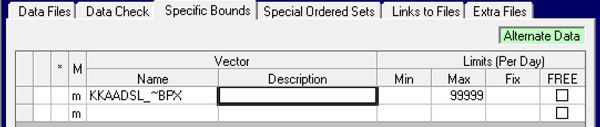
For something like this, which is a purchase or sale, simply add a Max (TABLE 1BP.0). This should at least give you a feasible solution, so that you can track down any pricing mistakes or missing limits.  Similarly if your unbounded vector represents an inventory or transportation option you can add a maximum where it was defined.

 

If your problem is a process unit (or recipe blend) operation, then a bound can be added on that mode, as here, which corresponds to TABLE 2(TN).4. If you are working in the database you need to remember that such unit changes apply to all cases where the unit is used, so if you are doing this for debugging it is a good idea to make a copy, either in the database or via the SSI, so you can get back to where you were.  Although with a process unit it may also be more obvious that there should be an active limit.  So, does your vector intersect with some loading rows?  If not, which ones should be involved?   If it does intersect, did you forget to constraint it?

Specification blending and pool quality vectors are a little harder to manage.  Just limiting the amount of the stream that can be blended or sold might resolve it.   If it’s a component-to-product option, then try a composition constraint.  If it’s a pool quality error vector, then a specification might take care of it.   If you are using quality penalties (RCPNLTY) to aid feasibility and the model goes unbounded on a quality, you should increase the penalty cost.  It is also possible to exempt properties from the penalty system via TABLES 500.9 and 600.9.

 

If you are not sure what the vector represents or cannot think where to limit, then you can use the Specific Bounds option (TABLE 196.0) to constrain it.   Just copy/paste the vector name in and try a value.  Report segment R1290 can help you keep track of active bounds.

 

Once you have a feasible solution, you can inspect it for issues, such as faulty pricing or inconsistent operations.   It is, of course, possible to have multiple causes of unbounded-ness in the same case.  (Take off all the process maxima and all the P/S constraints!).  As far as I can see, the optimizers only ever identify a single item; that is they stop as soon as they find the first problem.  However, if you are running a recursed model, sometimes the item identified is not the same on every pass which might give you more information about the nature of the problem.  If you add a constraint and the model remains unbounded, check to see if another vector has been identified and try again. 

 

Recursed models are sometimes unbounded on only some passes.   This means that some recursed elements take on values which upset the economics or break the structure.  For example, if you are recursing operating costs or utility consumptions they might switch sign.   If you have a mix of weight and volume purchase / sale options, changes in pool density can create economic incentives.   Another possibility is that a process constraint is effectively removed by setting a loading factor contribution to zero.  If these occur enough for you to worry or are associated with poor solutions, then you need to do some work with the PSI analyser to identify the combinations of inputs that create poor values, to improve your simulator input filtering or add some constraints on the outputs.   There aren’t any relevant desk notes on this sort of work (yet) but active clients can log on to tech support and look into the past conference papers where you will find a number of relevant presentations from myself and Richard Tan.

You want to reduce the risk of unbounded solutions? Then,  as Vince deVita a very experienced modeller from Jacobs Consulting, says  “Don’t let the model see infinity”.  Even if you are running what is intended to be a very open case, you should be able to imagine some sky high upper limit on the purchases and / or sales that would not normally be constraining.  (The optimizers, by the way, don’t like silly big values, so under 10E13.)   You might even find that these help the optimization process even when you are not going unbounded.  But don’t go crazy and limit absolutely every thing – or you just might go infeasible and make no money at all.